| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 자바 io 보조스트림
- 스레드
- 자바 입출력 스트림
- 쿠버네티스
- filewriter filereader
- container
- 리스트
- 컨테이너
- Kubernetes
- 김영한
- 동시성
- LIST
- 실전 자바 고급 1편
- Docker
- java network
- 멀티 쓰레드
- java socket
- 자료구조
- 자바
- Collection
- 스레드 제어와 생명 주기
- Thread
- java
- 인프런
- 도커 엔진
- Java IO
- 도커
- 쓰레드
- 알고리즘
- 시작하세요 도커 & 쿠버네티스
- Today
- Total
쌩로그
BOJ(백준) - 2231(분해합) 개념 정리 본문
해당 포스팅은 백준의 2231 - 분해합 문제에 대한 개념 정리다.
참고로 코드는 생략한다.(개념이 필요하지 코드가 필요한 건 아니라서 그렇다.)
구글링해본 결과 브루트 포스 알고리즘을 사용한다고 한다.
브루트 포스 알고리즘은 영어 뜻 그대로 브루트(무식한) 포스(힘) 즉 무식한 힘으로 해석된다.
쉽게 말해서 위의 문제를 예시로 들면 1부터 for문 돌리면서 분해합이 일치하는 것을 확인하면 결과를 반환한다는 것이다.
그리고 브루트 포스 알고리즘은 모든 경우의 수를 확인하기 때문에 완전 탐색 알고리즘이라고도 불린다.
문제는 다음과 같다.
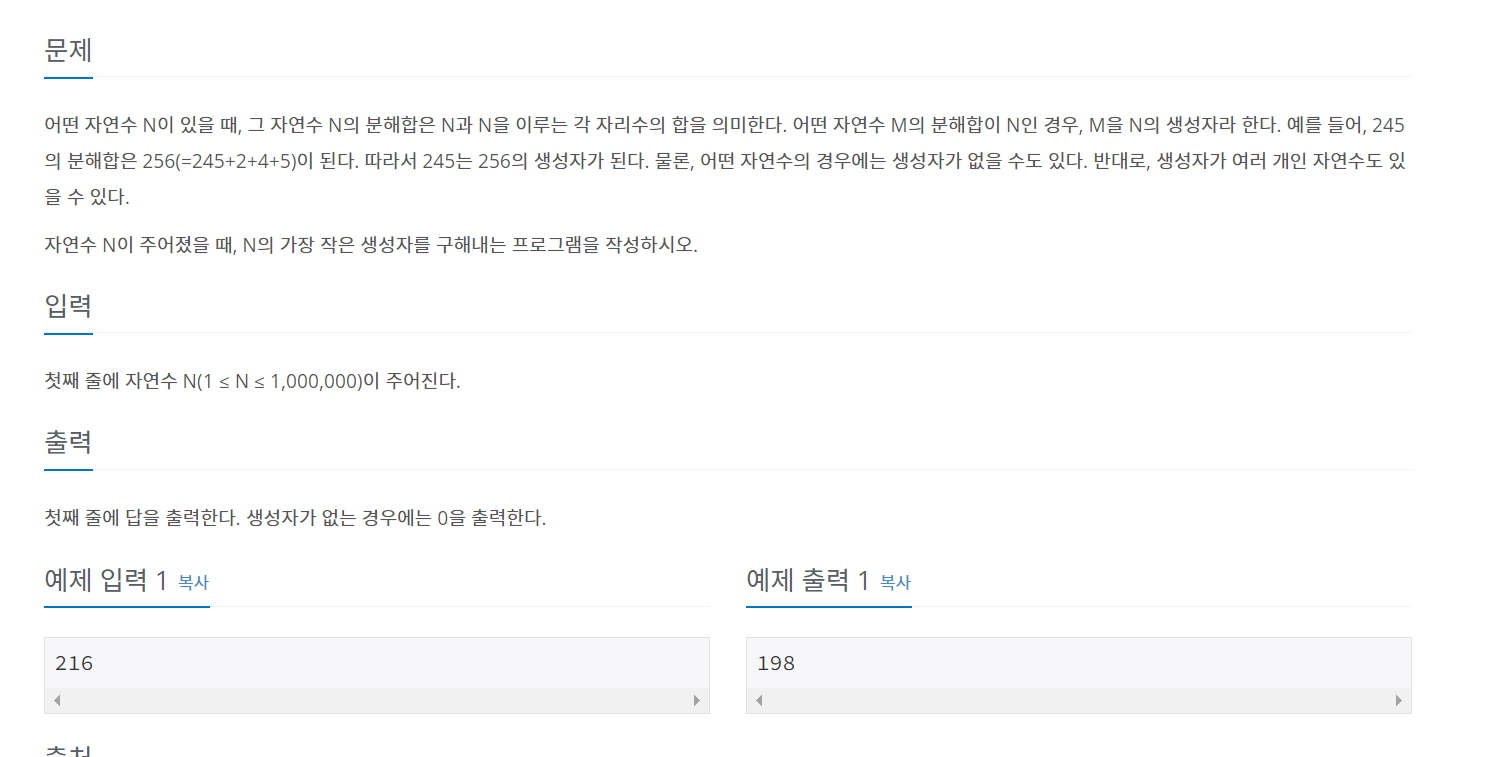
브루트 포스 알고리즘을 사용하면 1부터 198까지 for문을 돌리면서 아마 198을 도출했을 것이다.
그러나 브루트 포스 알고리즘도 다음과 같이 생각하면 더욱 더 효율적으로 사용할 수 있다.
어떤 수 A가 주어지면 A의 자리의 수를 합산하게 된다.
그 A와 A의 각 자리의 수를 합산한 수가 B라고 할 때 A는 B의 생성자가 된다는 것
위의 입출력 값을 예로 들면 216의 생성자가 198이 되는 이유는 198 + 1 + 9 + 8 이 216이기 때문이다.
만약 432 라면 어떨까?
지금은 알고리즘을 사용하지 않은 상태여서 어떤 수가 432의 생성자가 되는 수인지 알지 못한다.
하지만 범위는 알 수 있다.
각 자리수는 결국 1일 자리 수로 분해된다.
1의 자리수의 최댓값은 9이다.
그리고 생성자는 주어진 수(432)보단 분명히 작은 수여야 한다.
(그렇게 되야 생성자 + 생성자의 분해합이 432가 되기 때문이다.)
그리고 432는 세 자리 수이다.
세 자리 수이기 때문에 생성자인 B가 있다고 가정하면 B의 분해합의 최대값은 27을 넘지 못한다.
각 자리 수의 최댓값이 9이기 때문에 세 자리라면 9를 세 번 더한 27을 넘지 못한다.
(9 + 9 + 9)
최종적인 결론은 다음과 같다.
432 - 27 < 찾아야 할 생성자 < 432 라는 공식이 도출된다.
만약 6자리 수라면?
6자리수 - 6*9 < 찾아야 할 생성자 < 주어진 6자리 수 가 된다.
따라서 6자리 수라면
6자리수 - 54 부터 분해합을 찾아서 일치한 생성자를 출력하면 되고,
3자리 수라면
3자리수 -27 부터 분해합을 찾아서 일치한 생성자를 출력하면 된다.
따라서 주어진 수를 입력받았을 때 필요한 조건은 다음과 같다.
- 몇 자리 수인지
그리고 루프를 돌려서 생성자를 찾아서 있으면 해당 생성자를, 없으면 0을 출력하면 된다.

