| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- java
- 도커 엔진
- filewriter filereader
- Docker
- 컨테이너
- java socket
- 스레드 제어와 생명 주기
- 도커
- 알고리즘
- 동시성
- 리스트
- 스레드
- 자바
- 쿠버네티스
- 멀티 쓰레드
- Java IO
- 실전 자바 고급 1편
- java network
- 자료구조
- 자바 io 보조스트림
- Kubernetes
- LIST
- 김영한
- 자바 입출력 스트림
- Collection
- 인프런
- container
- 쓰레드
- 시작하세요 도커 & 쿠버네티스
- Thread
- Today
- Total
쌩로그
김영한의 실전 자바 - 중급 2편 - Sec 09. 컬렉션 프레임워크 - Set 본문
목차
- 포스팅 개요
- 본론
2-1. 자바가 제공하는 Set1 - HashSet, LinkedHashSet
2-2. 자바가 제공하는 Set2 - TreeSet
2-3. 자바가 제공하는 Set3 - 예제
2-4. 자바가 제공하는 Set4 - 최적화 - 요약
1. 포스팅 개요
해당 포스팅은 김영한의 실전 자바 중급 2편 Section 9의 컬렉션 프레임워크 - Set 에 대한 학습 내용이다.
학습 레포 URL : https://github.com/SsangSoo/inflearn-holyeye-java-mid2 (해당 레포는 완강시 public으로 전환 예정이다.)
2. 본론
2-1. 자바가 제공하는 Set1 - HashSet, LinkedHashSet
셋은 중복을 허용하지 않고, 순서를 보장하지 않는 자료 구조이다.
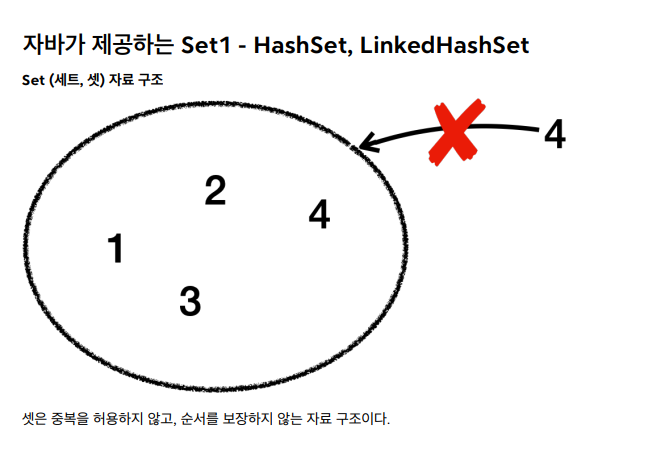
컬렉션 프레임워크 - Set
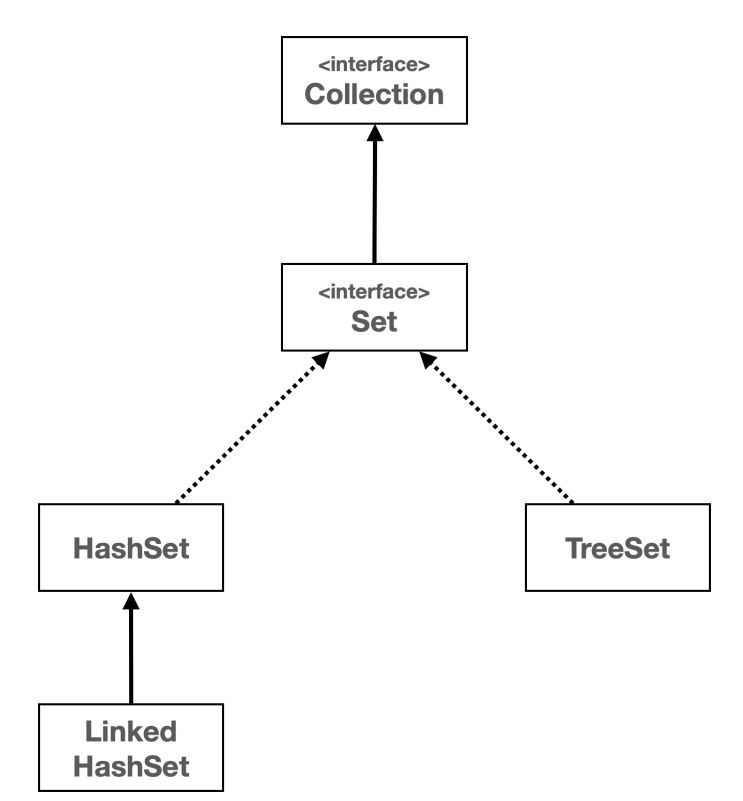
Collection 인터페이스Collection 인터페이스는 java.util 패키지의 컬렉션 프레임워크의 핵심 인터페이스 중 하나이다.
이 인터페이스는 자바에서 다양한 컬렉션, 즉 데이터 그룹을 다루기 위한 메서드를 정의한다.Collection 인터페이스는 List , Set , Queue 와 같은 다양한 하위 인터페이스와 함께 사용되며, 이를 통해 데이터를 리스트, 세트, 큐 등의 형태로 관리할 수 있다.
Set 인터페이스
자바의 Set 인터페이스는 java.util 패키지의 컬렉션 프레임워크에 속하는 인터페이스 중 하나이다.Set 인터페이스는 중복을 허용하지 않는 유일한 요소의 집합을 나타낸다.
즉, 어떤 요소도 같은 Set 내에 두 번 이상 나타날 수 없다.Set 은 수학적 집합 개념을 구현한 것으로, 순서를 보장하지 않으며, 특정 요소가 집합에 있는지 여부를 확인하는 데 최적화되어 있다.
Set 인터페이스는 HashSet , LinkedHashSet , TreeSet 등의 여러 구현 클래스를 가지고 있으며, 각 클래스는 Set 인터페이스를 구현하며 각각의 특성을 가지고 있다.
Set 인터페이스의 주요 메서드
| 메서드 | 설명 |
|---|---|
add(E e) |
지정된 요소를 세트에 추가한다(이미 존재하는 경우 추가하지 않 음). |
addAll(Collection<? extends E> c) |
지정된 컬렉션의 모든 요소를 세트에 추가한다. |
contains(Object o) |
세트가 지정된 요소를 포함하고 있는지 여부를 반환한다. |
containsAll(Collection<?> c) |
세트가 지정된 컬렉션의 모든 요소를 포함하고 있는지 여부를 반환한다. |
remove(Object o) |
지정된 요소를 세트에서 제거한다. |
removeAll(Collection<?> c) |
지정된 컬렉션에 포함된 요소를 세트에서 모두 제거한다. |
retainAll(Collection<?> c) |
지정된 컬렉션에 포함된 요소만을 유지하고 나머지 요소는 세트 에서 제거한다 |
clear() |
세트에서 모든 요소를 제거한다. |
size() |
세트에 있는 요소의 수를 반환한다. |
isEmpty() |
세트가 비어 있는지 여부를 반환한다 |
iterator() |
세트의 요소에 대한 반복자를 반환한다. |
toArray() |
세트의 모든 요소를 배열로 반환한다. |
toArray(T[] a) |
세트의 모든 요소를 지정된 배열로 반환한다. |
Set의 구현체
HashSetLinkedHashSetTreeSet
1. HashSet
- 구현 : 해시 자료 구조를 사용해서 요소를 저장한다.
- 순서 : 요소들은 특정한 순서 없이 저장된다. 즉, 요소를 추가한 순서를 보장하지 않는다.
- 시간 복잡도 :
HashSet의 주요 연산(추가, 삭제, 검색)은 평균적으로O(1)시간 복잡도를 가진다. - 용도 : 데이터의 유일성만 중요하고, 순서가 중요하지 않은 경우에 적합하다.
HashSet 구현
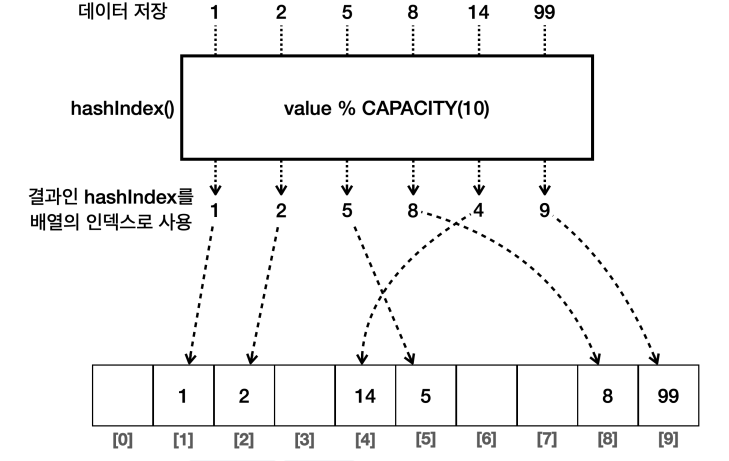
2. LinkedHashSet
- 구현 :
LinkedHashSet은HashSet에 연결 리스트를 추가해서 요소들의 순서를 유지한다. - 순서 : 요소들은 추가된 순서대로 유지된다. 즉, 순서대로 조회 시 요소들이 추가된 순서대로 반환된다.
- 시간 복잡도 :
LinkedHashSet도HashSEt과 마찬가지로 주요 연산에 대해 평균O(1)시간 복잡도를 가진다. - 용도 : 데이터의 유일성과 함께 삽입 순서를 유지해야 할 때 적합하다.
- 참고 : 연결 링크를 유지해야 하기 때문에 성능상
HashSet보다는 조금 더 무겁다.
LinkedHashSet 구현
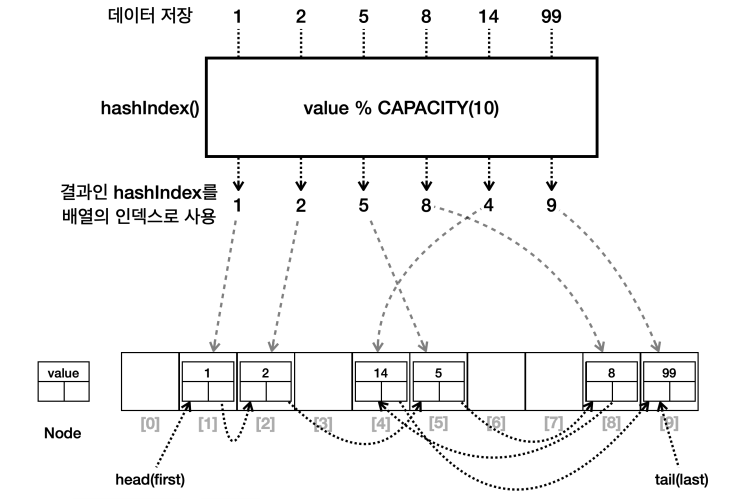
LinkedHashSet은HashSet에 연결 링크만 추가한 것이다.HashSet에LinkedList를 합친 것으로 이해하면 된다.- 이 연결 링크는 데이터를 입력한 순서대로 연결된다.
had(first)부터 순서대로 링크를 따라가면 입력 순서대로 데이터를 순회할 수 있다.- 양방향으로 연결된다. (그림은 단방향이지만, 실제로는 양방향이다.)
first부터 순서대로 따라가면서 출력한다면 순서대로 출력할 수 있다.
2-2. 자바가 제공하는 Set2 - TreeSet
이어서 TreeSet이다.
3. TreeSet
- 구현 :
TreeSet은 이진 탐색 트리를 개선한 레드-블랙 트리를 내부에서 사용한다.- 자바 버전에 따라 달라질 수 있다.
- 순서 : 요소들은 정렬된 순서로 저장된다. 순서의 기준은 비교자(
Comparator)로 변경할 수 있다. - 시간 복잡도 : 주요 연산들은
O(log n)의 시간 복잡도를 가진다. 따라서HashSet보다는 느리다. - 용도 : 데이터들은 정렬된 순서로 유지하면서 집합의 특성을 유지해야 할 때 사용한다.
- 예를 들어, 범위 검색이나 정렬된 데이터가 필요한 경우에 유용하다.
- 순서는 입력된 순서가 아니라, 데이터 값의 순서다.
트리 구조
TreeSet 을 이해하려면 트리 구조를 먼저 알아야 한다.
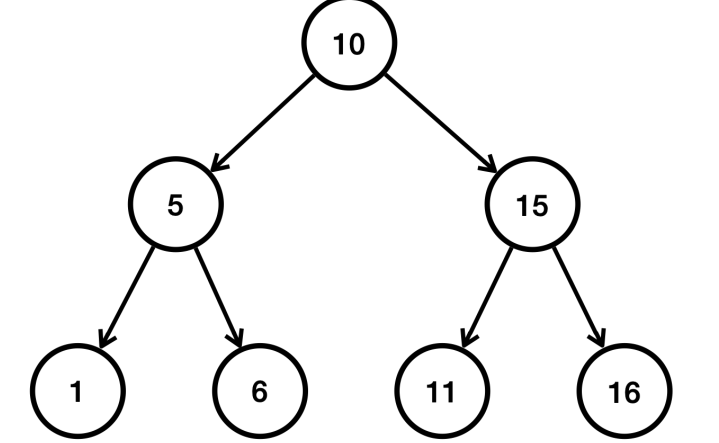
- 트리는 부모 노드와 자식 노드로 구성된다.
- 가장 높은 조상을 루트(root)라 한다.
- 자식이 2개까지 올 수 있는 트리를 이진 트리라 한다.
- 여기에 노드의 왼쪽 자손은 더 작은 값을 가지고, 오른쪽 자손은 더 큰 값을 가지는 것을 이진 탐색 트리라 한다.
TreeSet은 이진 탐색 트리를 개선한 레드-블랙 트리를 사용한다.
트리 구조의 구현
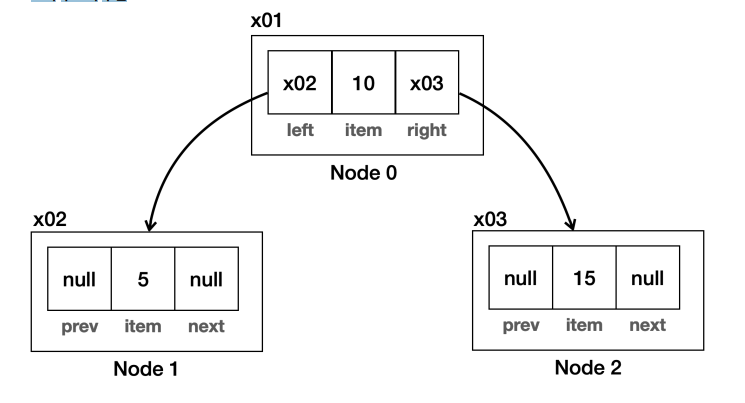
class Node {
Object item;
Node left;
Node right;
}- 트리 구조는 왼쪽, 오른쪽 노드를 알고 있으면 된다.
- 앞서 다룬 연결 리스트의 구현을 떠올려보면 쉽게 이해가 될 것이다.
이진 탐색 트리 - 입력 예시
이진 탐색 트리의 핵심은 데이터를 입력하는 시점에 정렬해서 보관한다는 점이다.
그리고 작은 값은 왼쪽에 큰 값은 오른쪽에 저장하면 된다.
데이터를 10, 5, 15, 1, 6, 11, 16 순서대로 입력한다고 가정했을 때. 처음에 10을 입력했다고 가정하고. 다음으로 5, 15를 입력한다.
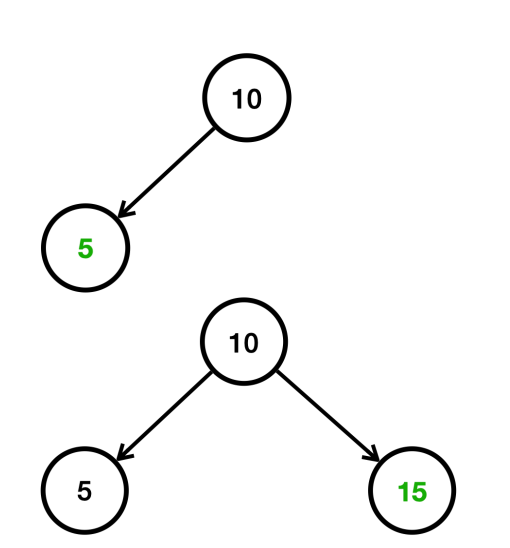
- 5는 10보다 작으므로 왼쪽에 저장된다.
- 15는 10보다 크므로 오른쪽에 저장된다
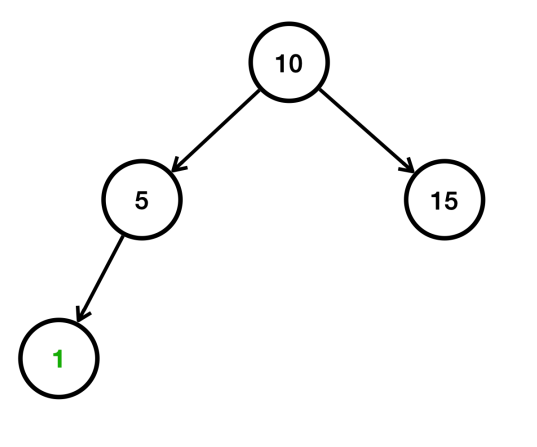
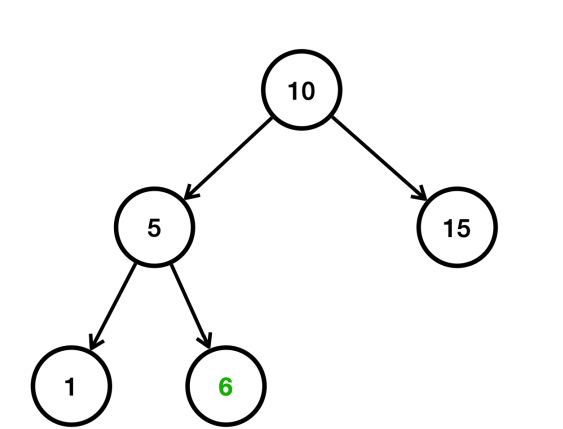
- 1은 10보다 작다. 따라서 왼쪽으로 찾아간다. 1은 5보다 작다 따라서 왼쪽에 저장된다.
- 6은 10보다 작다. 따라서 왼쪽으로 찾아간다. 6은 5보다 크다. 따라서 오른쪽에 저장된다.
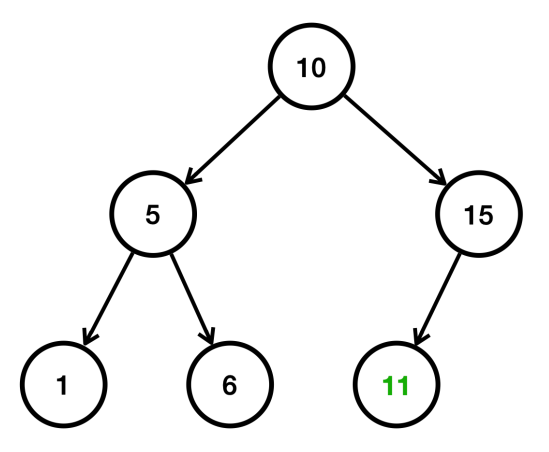
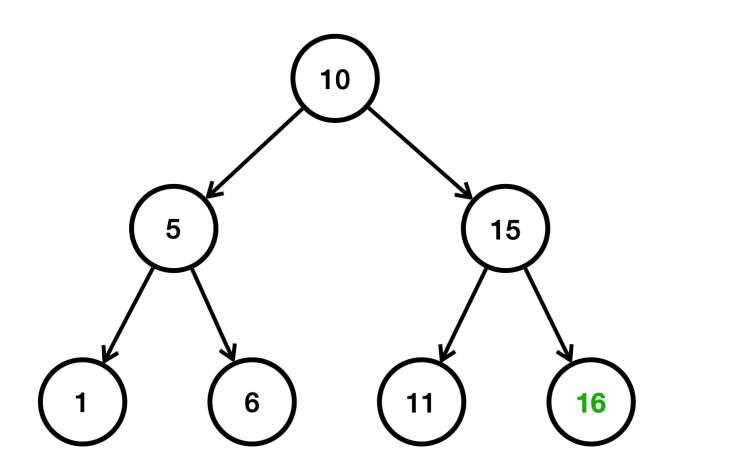
- 11은 10보다 크다. 따라서 오른쪽으로 찾아간다. 11은 15보다 작다. 따라서 왼쪽에 저장된다.
- 16은 10보다 크다. 따라서 오른쪽으로 찾아간다. 16은 15보다 크다. 따라서 오른쪽에 저장된다.
이진 탐색 트리 - 검색
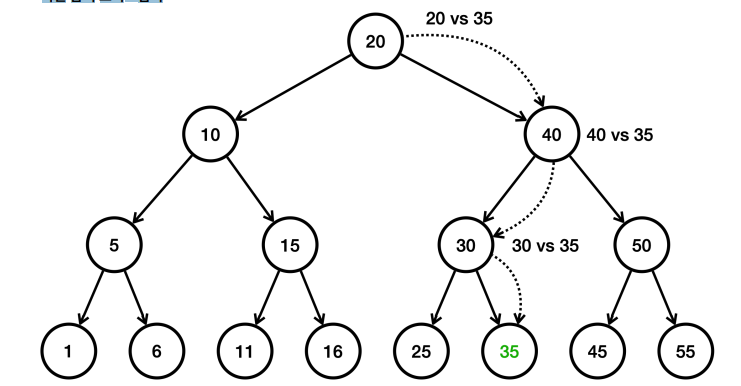
- 여기에는 총 15개의 데이터가 들어있다. 여기서 숫자 35를 검색한다고 가정한다.
- 1번: 루트인 20과 35를 비교한다. 35가 더 크므로 오른쪽으로 찾아간다.
- 2번: 40과 35를 비교한다. 35가 더 작으므로 왼쪽으로 찾아간다.
- 3번: 30과 35를 비교한다. 35가 더 크므로 오른쪽으로 찾아간다.
- 4번: 노드에 있는 값을 비교한다. 35와 같으므로 35를 찾는다.
데이터가 총 15개인데 4번의 계산으로 필요한 결과를 얻을 수 있었다.
이것은 O(n) 인 리스트의 검색보다는 빠르고, O(1)인 해시의 검색 O(1)보다는 느리다.
- 리스트의 경우
O(n)이므로 15번의 연산이 필요하다. - 해시 검색은
O(1)이므로 1번의 연산이 필요하다.
이진 탐색 트리 계산의 핵심은 한번에 절반을 날린다는 점이다. 계산을 단순화 하기 위해 16개의 데이터가 있다고 가정하면.
- 16개의 데이터가 있다. 루트에서 처음 비교를 통해 절반의 데이터를 찾지 않아도 된다. 따라서 16 / 2 = 8이 된다.
- 8개의 데이터가 있다. 비교를 통해 절반의 데이터만 남는다. 따라서 8 /2 = 4가 된다.
- 4개의 데이터가 있다. 비교를 통해 절반의 데이터만 남는다. 따라서 4 / 2 = 2가 된다.
- 2개의 데이터가 있다. 비교를 통해 절반의 데이터만 남는다. 따라서 2 / 2 = 1이 된다.
- 1이 남았으므로 이 값이 맞는지 확인하면 된다.
이진 탐색 트리의 빅오 - O(log n)
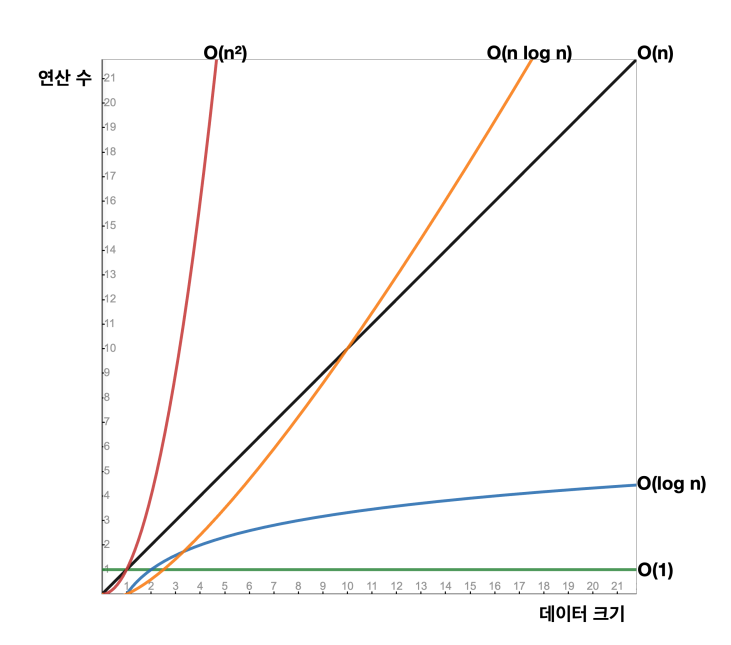
16개의 경우 단 4번의 비교 만으로 최종 노드에 도달할 수 있다. 이것을 정리하면 다음과 같다.
- 2개의 데이터 => 2로 1번 나누기,
log₂(2)=1 - 4개의 데이터 => 2로 2번 나누기,
log₂(4)=2 - 8개의 데이터 => 2로 3번 나누기,
log₂(8)=3 - 16개의 데이터 => 2로 4번 나누기,
log₂(16)=4 - 32개의 데이터 => 2로 5번 나누기,
log₂(32)=5 - 64개의 데이터 => 2로 6번 나누기,
log₂(64)=6 - ...
- 1024개의 데이터 => 2로 10번 나누기,
log₂(1024)=10
1024개의 데이터를 단 10번의 계산으로 원하는 결과를 찾을 수 있다.
데이터의 크기가 늘어나도 늘어난 만큼 한 번의 계산에 절반을 날려버리기 때문에, O(n)과 비교해서 데이터의 크기가 클수록 효과적이다
이것을 수학으로 log₂(n) 으로 표현한다(수학 공식이 핵심이 아니다).
로그는 쉽게 이야기해서 2로 몇 번 나누어서 1에 도달할 수 있는지 계산하면 된다.
빅오 표기법에서 상수는 사용하지 않으므로 상수를 제외하고 단순히 O(log n) 로 표현한다.
이진 탐색 트리와 성능
이진 탐색 트리의 검색, 삽입, 삭제의 평균 성능은 O(log n) 이다.
하지만 트리의 균형이 맞지 않으면 최악의 경우 O(n)의 성능이 나온다.
만약 데이터를 1, 5, 6, 10, 15 순서로 입력했다고 가정해보자.
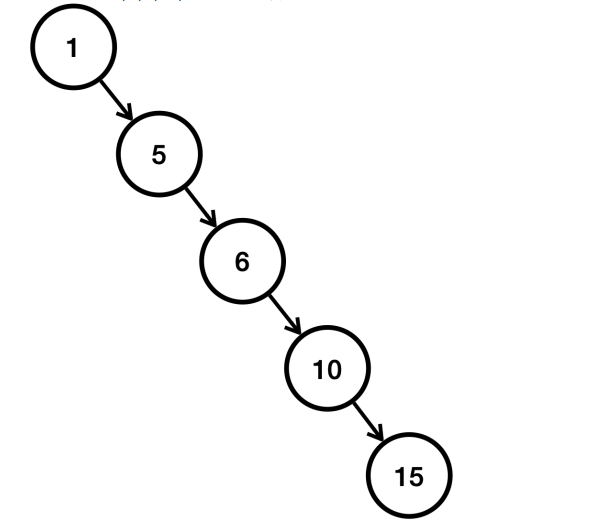
- 이렇게 오른쪽으로 치우치게 되면, 결과적으로 15를 검색 했을 때 데이터의 수인 5만큼 검색을 해야 한다.
- 따라서 이런 최악의 경우 O(n)이 성능이 나온다.
이진 탐색 트리 개선
이런 문제를 해결하기 위한 다양한 해결 방안이 있는데 트리의 균형이 너무 깨진 경우 동적으로 균형을 다시 맞추는 것이다.
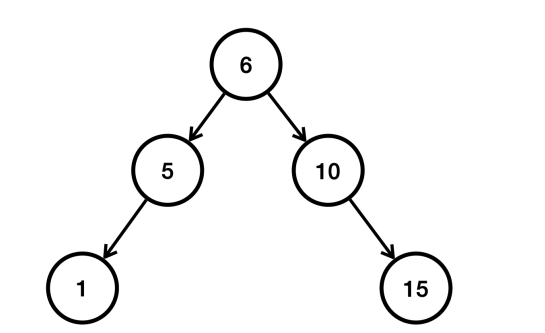
- 중간에 있는 6을 기준으로 다시 정렬한다.
- AVL 트리, 레드-블랙 트리 같은 균형을 맞추는 다양한 알고리즘이 존재한다.
- 자바의
TreeSet은 레드-블랙 트리를 사용해서 균형을 지속해서 유지한다. 따라서 최악의 경우에도O(log n)의 성능을 제공한다.
이진 탐색 트리 - 순회
- 이진 탐색 트리의 핵심은 입력 순서가 아니라, 데이터의 값을 기준으로 정렬해서 보관한다는 점이다.
- 따라서 정렬된 순서로 데이터를 차례로 조회할 수 있다. (순회 할 수 있다.)
- 데이터를 차례로 순회하려면 중위 순회라는 방법을 사용하면 된다. 왼쪽 서브트리를 방문한 다음, 현재 노드를 처리하고, 마지막으로 오른쪽 서브트리를 방문한다. 이 방식은 이진 탐색 트리의 특성상, 노드를 오름차순(숫자가 점점 커짐)으로 방문한다.
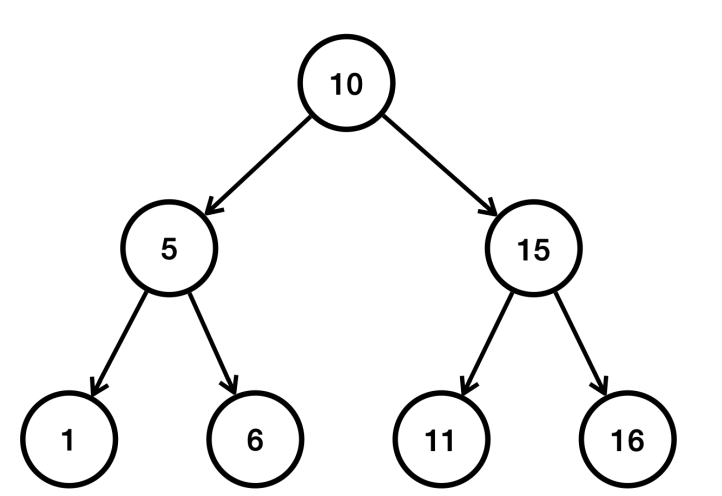
중위 순회 순서
자신의 왼쪽의 모든 노드를 처리하고, 자신의 노드를 처리하고, 자신의 오른쪽 모든 노드를 처리하는 방식이다.
- 10의 기준에서 왼쪽 서브트리를 방문한다.
- 5의 기준에서 왼쪽 서브트리를 방문한다.
- 1을 출력한다.
- 5 자신을 출력한다.
- 5의 기준으로 오른쪽 서브트리를 방문한다.
- 6을 출력한다.
- 5의 기준에서 왼쪽 서브트리를 방문한다.
- 10 자신을 출력한다.
- 10의 기준에서 오른쪽 서브트리를 방문한다.
- 15의 기준에서 왼쪽 서브트리를 방문한다.
- 11을 출력한다.
- 15 자신을 출력한다.
- 15의 기준으로 오른쪽 서브트리를 방문한다.
- 16을 출력한다.
- 15의 기준에서 왼쪽 서브트리를 방문한다.
순서대로 1, 5, 6, 10, 11, 15, 16이 출력된다.
2-3. 자바가 제공하는 Set3 - 예제
자바가 제공하는 HashSet , LinkedHashSet , TreeSet 을 코드로 확인한다.
public class JavaSetMain {
public static void main(String[] args) {
run(new HashSet<>());
run(new LinkedHashSet<>());
run(new TreeSet<>());
}
private static void run(Set<String> set) {
System.out.println("set = " + set.getClass());
set.add("C");
set.add("B");
set.add("A");
set.add("1");
set.add("2");
Iterator<String> iterator = set.iterator();
while(iterator.hasNext()) {
System.out.print(iterator.next() + " ");
}
System.out.println();
}
}
// 결과
set = class java.util.HashSet
A 1 B 2 C
set = class java.util.LinkedHashSet
C B A 1 2
set = class java.util.TreeSet
1 2 A B C HashSet: 입력한 순서를 보장하지 않는다.LinkedHashSet: 입력한 순서를 정확히 보장한다.TreeSet: 데이터 값을 기준으로 정렬한다.
2-4. 자바가 제공하는 Set4 - 최적화
자바 HashSet과 최적화
- 자바의
HashSet은 우리가 직접 구현한 내용과 거의 같지만 다음과 같은 최적화를 추가로 진행한다.
최적화
- 해시 기반 자료 구조를 사용하는 경우 통계적으로 입력한 데이터의 수가 배열의 크기를 75% 정도 넘어가면 해시 인덱스가 자주 충돌한다. 따라서 75%가 넘어가면 성능이 떨어지기 시작한다.
- 해시 충돌로 같은 해시 인덱스에 들어간 데이터를 검색하려면 모두 탐색해야 한다. 따라서 성능이 O(n)으로 좋지 않다.
- 하지만 데이터가 동적으로 계속 추가되기 때문에 적절한 배열의 크기를 정하는 것은 어렵다.
- 자바의
HashSet은 데이터의 양이 배열 크기의 75%를 넘어가면 배열의 크기를 2배로 늘리고 2배 늘어난 크기를 기준으로 모든 요소에 해시 인덱스를 다시 적용한다.- 해시 인덱스를 다시 적용하는 시간이 걸리지만, 결과적으로 해시 충돌이 줄어든다.
- 자바
HashSet의 기본 크기는16이다.
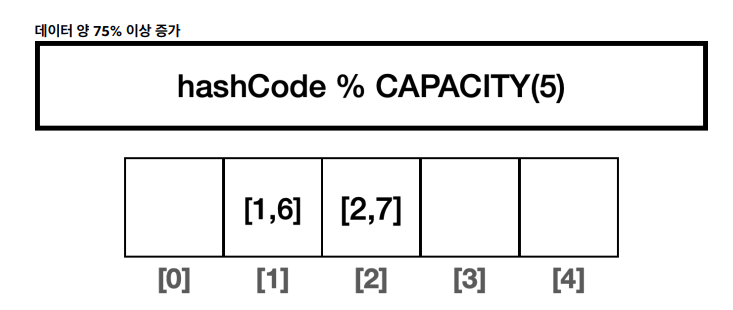
- 데이터 양이 75% 이상 증가하면 그 만큼 해시 인덱스의 충돌 가능성도 높아진다.
배열의 크기 2배 증가 후, 해시 다시 계산
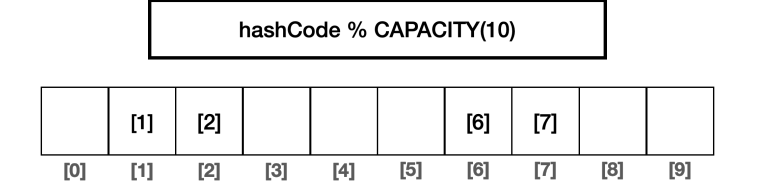
- 데이터양이 75% 이상이면 배열의 크기를 2배로 증가하고, 모든 데이터의 해시 인덱스를 커진 배열에 맞추어 다시 계산한다. 이 과정을 재해싱(rehashing)이라 한다.
- 인덱스 충돌 가능성이 줄어든다.
- 여기서 데이터가 다시 75% 이상 증가하면 다시 2배 증가와 재계산을 반복한다.
정리
실무에서는 Set 이 필요한 경우 HashSet 을 가장 많이 사용한다.
그리고 입력 순서 유지, 값 정렬의 필요에 따라서 LinkedHashSet , TreeSet 을 선택하면 된다.
3. 요약
자바에서 제공하는 Set 인터페이스에 대한 개념과 구현체가 어떤 것들이 있는지에 대해 자세히 알아보았다.
'Language > JAVA' 카테고리의 다른 글
| 김영한의 실전 자바 - 중급 2편 - Sec 11. 컬렉션 프레임워크 - 순회, 정렬, 전체 정리 (1) | 2025.02.03 |
|---|---|
| 김영한의 실전 자바 - 중급 2편 - Sec 10. 컬렉션 프레임워크 - Map, Stack, Queue (1) | 2025.01.29 |
| 김영한의 실전 자바 - 중급 2편 - Sec 08. 컬렉션 프레임워크 - HashSet (0) | 2025.01.23 |
| 김영한의 실전 자바 - 중급 2편 - Sec 07. 컬렉션 프레임워크 - 해시(Hash) (1) | 2025.01.18 |
| 김영한의 실전 자바 - 중급 2편 - Sec 06. 컬렉션 프레임워크 - List (0) | 2025.01.16 |
